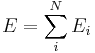Random energy model

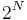In statistical physics of disordered systems, the random energy model is a toy model of a system with quenched disorder. It concerns the statistics of a system of $N$ particles, such that the number of possible states for the systems grow as $2^N$ , while the energy of such states is a Gaussian stochastic variable. The model has an exact solution. Its simplicity makes this model suitable for pedagogical introduction of concepts like quenched disorder and replica symmetry.

Comparison with other disordered systems

The 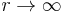$r\to \infty$ limit of the Infinite Range Model is known as the Random energy model.

Derivation of thermodynamical quantities

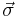As its name suggests, the REM has an independent distribution of energy. For a particular realization of the disorder, $P(E) = \delta(E - H[\vec{\sigma}])$ where $\vec{\sigma}$ refers to the set of individual spin configurations described by the state and $H[\vec{\sigma}]$ is the energy associated with it due to spin-spin interactions, which can be of different types for different pairs of spins. Since there is disorder in the system, the final extensive variables like free energy need to be averaged over all possible types of magnetic links between all spins, just as in the case of the Edwards Anderson model. 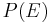Averaging $P(E)$ for a single realization of the disorder, over all possible realizations along with a gaussian probability distribution, we find the probability of the disordered system having an energy $E$ :

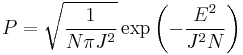
$P = \sqrt{\dfrac{1}{N\pi J^{2}}}\exp\left(-\dfrac{E^{2}}{J^{2}N}\right)$

it can be seen that the probability of the spin glass existing in a particular state, does not depend only on the energy of that state and not on the individual spin configurations in it^[1].

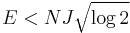The entropy of the REM is given by^[2] $S(E) = N\left[\log 2 - \left(\dfrac{E}{NJ}\right)^{2}\right]$ for $E < NJ\sqrt{\log 2}$ .

Suppose a system is described by a total energy given by a sum of random energy

$E = \sum_i^N E_i$

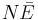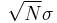suppose that these are independent and identical random variables with average $\bar{E}$ and standard deviation $\sigma$ , then by the central limit theorem the energy E will be a random variable with gaussian distribution with mean $N \bar{E}$ and standard deviation $\sqrt{N} \sigma$ .

References

^ Nishimori, Hidetoshi (2001). Statistical Physics of Spin Glasses and Information Processing: An Introduction. Oxford: Oxford University Press. pp. 243. ISBN 0198509405, 9780198509400. http://preterhuman.net/texts/science_and_technology/physics/Statistical_physics/Statistical%20physics%20of%20spin%20glasses%20and%20information%20processing%20an%20introduction%20-%20Nishimori%20H..pdf.
^ Derrida, Bernard (01). Random-energy model: An exactly solvable model of disordered systems. Phys. Rev. B. 24. Bibcode 1981PhRvB..24.2613D. doi:10.1103/PhysRevB.24.2613. http://link.aps.org/doi/10.1103/PhysRevB.24.2613. Retrieved 24 March 2011.